
Turinys
Bendra prielaida, kad titulinis tvarinys yra Ataka ant Titano: Laisvės sparnai tai, kad jie yra žmonės, išsiplėtę ir dažniausiai beprasmiški. Kai kurie neturi odos, todėl jie tampa baisesni, bet tai ne vienintelis dalykas, dėl kurio jie skiriasi nuo kitų, kurie yra gigantai. Jie turi nepasotinamą apetitą žmonėms. Ir šie tvariniai yra visa priežastis, dėl kurios miesto aplinkoje buvo sukurtos trys milžiniškos sienos. Tai yra priežastis, dėl kurios praėjusią savaitę paminėjo 3D manevravimo įrankius. Ir jei mes esame sąžiningi su savimi, tai yra priežastis, dėl kurios susidomėjome „Titan“ ataka franšizę.
Daugelis žmonių jau kalbėjo apie gigantų mokslą, ir aš tikrai apie tai kalbėsiu dar kartą, nes labai svarbu suprasti gigantų fiziką ir kodėl tam tikri gyvūnai auga taip aukšti, kaip jie daro ir kodėl kiti ne. Tačiau, mano tikrasis ketinimas šio savaitės straipsnyje, yra atsakyti į kitą klausimą: kaip didelis „Titan“ gali realiai gauti? Taigi dar kartą suprasime šūdą Ataka ant Titano: Laisvės sparnai.
„Galileo“ sako
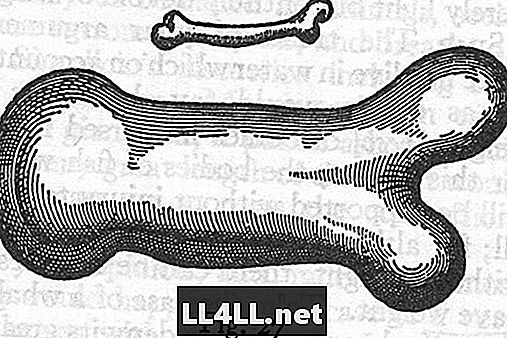
Visi girdėjome apie „Galileo“, tiesa. Vaikinas, kuris daug žvelgė į dangų. Na, jis buvo žinomas daugiau nei jo astronomija. Jis iš tikrųjų buvo genijus matematikas. Be to, jis buvo nuostabus stebėtojas. Savo knygoje Du nauji mokslai, jis kalba apie du laivus, abu yra identiški. Nuo stiebo iki denio ir nuo laivapriekio iki laivagalio nebuvo skirtumų, išskyrus vieną: vienas yra du kartus didesnis už kitą. Jis pastebi, kad didesniam laivui reikės daugiau pastolių ir stabilizuoti, kad jis nesumaltų pagal savo svorį.
Bet tai neturi prasmės? Tai tik didesnis; ji turėtų turėti tas pačias fizines savybes kaip ir mažesnis, tiesa? Deja, šis teiginys yra neteisingas. Pagrindiniame lygmenyje kiekviename objekte esantys atomai yra tokie patys, tačiau didesniame elemente yra daugiau atomų, tačiau praktiškiau geometrija keičiasi su didesniu objektu.
Įsivaizduokite, kad kubas yra 1 cm 1 cm, jo tūris yra 1 cm³ arba 1 l, o jo masė yra maždaug 1 g, jei užpildyta vandeniu. Kiek vandens būtų 10 cm kubas? Jei manote, kad yra 10 cm³ ar net 100 cm³, jums būtų neteisinga. Jame būtų 1000 cm³. Be to, masė tris kartus padidėjo proporcingai iki 1000 g. Tai vadinama „Galileo“ aikštės kubo teise.
Titanas yra žmogaus proporcija, bet stovintis maždaug 15 m aukštyje. Jei vidutinis žmogus yra apie 1,5 m (žr. Kur aš einu?), Tada Titanas yra 10 kartų didesnis už aukštį. Jei mes apvalinsime vidutinį 1,5 m žmogaus svorį iki 70 kg. Tai reiškia, kad žmogaus formos milžinas, kurio aukštis būtų 10 kartų didesnis, turėtų 1 000 kartų didesnę masę, 70 000 kg. Beje, tai yra 70 metrinių tonų. Be jokios papildomos paramos struktūros, „Titan“ būtų susmulkintas pagal savo svorį, jau nekalbant apie stiprumą, kurį ji imtųsi, kad per tą sistemą perkrautų daug kraujo.
Šoninėje pastaboje, kai pjaustote titaną ant kaklo nugaros, jis išpurškia kraują. Jūs suprantate, kad jei jūsų personažas bus nukentėjęs nuo to kūno skysčių srauto, jis būtų panašus į nukentėjusį nuo visiškai atidarytos ugnies žarnos.

„Galileo“ savo knygoje sakė: „Galiausiai, galime sakyti, kad kiekvienai mašinai ir struktūrai, tiek dirbtinai, tiek natūraliai, yra nustatyta būtina riba, kurią viršijus nei menas, nei gamta negali praeiti; Žinoma, čia suprantama, kad medžiaga yra tokia pati ir išsaugota proporcija. “Kitaip tariant, viskas yra struktūrinis apribojimas. Kokie yra žmogaus rėmo apribojimai? Dėl kintamųjų skaičiaus ketinu laikytis rėmo, o ne kraujotakos sistemos ar kitos tokios sistemos, tačiau žinau, kad daugelis šių ribų yra daug mažesnės už vidinį struktūrinį vientisumą. Tikimės, kad dirbame su geriausiu atveju.
Aukščiausias žmogus, kada nors gyvenantis, gimė Altone, IL, tik truputį nuo mano vaikystės namų St. Louis'e. Jo vardas buvo Robert Wadlow. Jis buvo pilnas 8 pėdos (2,7178 m). Daugiau nei metras aukščiau nei vidutinis žmogus. Ir nepaisant to, kad jis buvo labai liesas, jis sverdavo 220 kg, tris kartus daugiau nei vidutinis žmogus. Wadlow netgi turėjo nešioti specialias petnešos ant kojų, kad jam suteiktų papildomą paramą jo masei. Deja, Wadlow mirė labai jauname 22 metų dėl komplikacijų dėl jo aukščio.
„Galileo“ teigė, kad kaulų struktūra, kuri yra dvigubai didesnė už žmogaus aukštį, turėtų būti maždaug keturis kartus storesnė. Jis netgi nupiešė kojų kaulą. Tačiau vis dar kyla problemų dėl to, kad jį naudojote titane, kai manote, kad kaulų streso riba yra apskritai.
Žmogaus kaulų stiprumas yra apie 4 400 MN / m², o tai reiškia, kad jei slėgis virš kaulų yra daugiau nei 4000 NM, jis bus susmulkintas. Žmonėms vaikščiojant, vidutiniškai žmogus turi 55 MN / m² arba 110 MN / m² kaulų. Tačiau „Titan“, sveriantis 70 tonų, įdėti 110 000 MN / m², jei atliktume paprastą santykį.
Realiai, „Titan“ tikriausiai nebūtų daug didesnis nei Wadlow, apie 3 metrai, bet kur tai įdomus? Leiskite man žinoti, ką jūs manote komentaruose, ir leiskite man žinoti, kas atsitinka, kai jūs išmatosite tai.
